Symbolic Calculator
For iPhone, iPod Touch and iPad
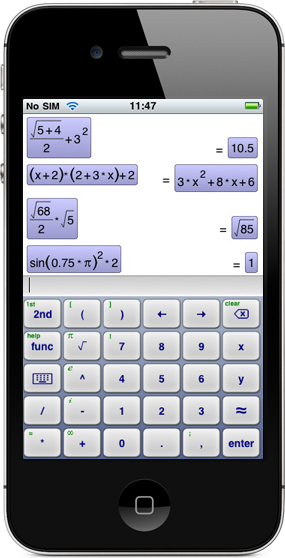
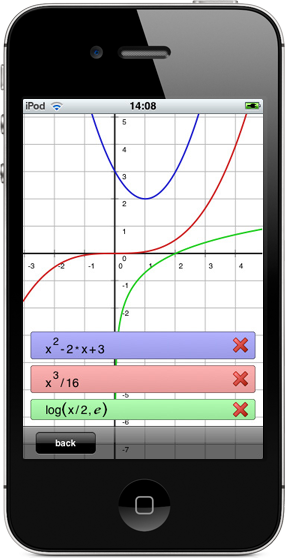
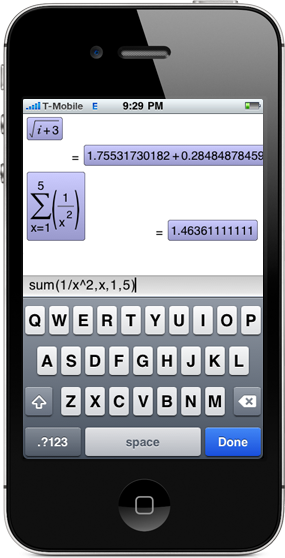
The perfect math app with full-featured algebra capabilites on par with high-end scientific calculators, ideal for high-school or college students, engineers or anyone needing a powerful math toolbox. Even if you are using just a fraction of the functionalities, the iphone-ish, easy-to-use interface makes life much easier compared to traditional calculators.
- Exact arithmetic (unless you select rounded numerical mode)
- Formulas displayed in "natural" form
- History, storing results in an easy-to-use way
- Unlimited number of variables, user-defined functions
- Session management
- Simplifying or expanding expressions
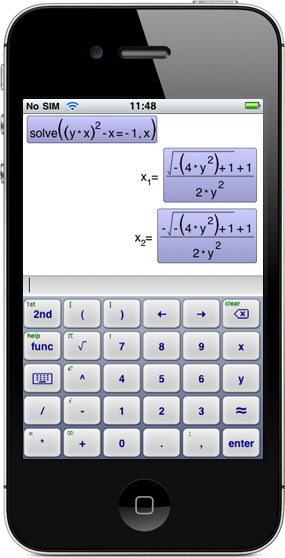
- Solving equations, systems, differential equations, numerically or symbolically
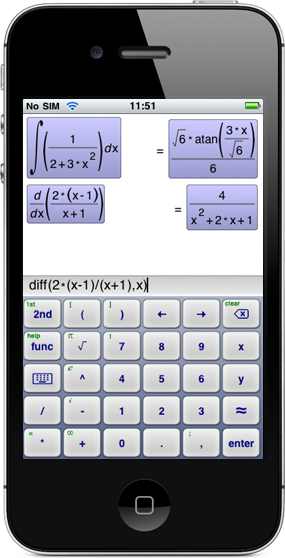
- Integrals, derivatives, limits, taylor series, etc for function analysis
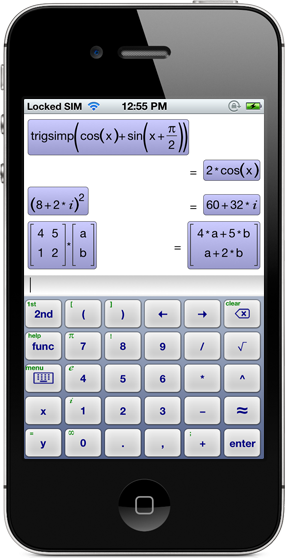
- Full support for complex numbers
- Vectors, matrices, linear algebra functions
for iPhone and iPad:
for android:
Note that this video was made with an earlier version of the app
so there are some differences, but it still illustrates
the basic concepts of the user interface.
If you would like to read the in-app help on an other device while running the app, you can access the help files from here:
iPhone version
iPad version
Additionally here is a list of built-in functions. Click on one of them to see the details. (this is the same as what you get when pressing the question mark in the function list)
abs(expr)
Absolute value of a number
Examples:
abs(-6)=6
abs(3+4*i)=5
Examples:
abs(-6)=6
abs(3+4*i)=5
asin(expr)
Arc sine. Result is in radian or degree depending on the selected trigonometric mode.
asinh(expr)
Area hyperbolic sine.
acos(expr)
Arc cosine. Result is in radian or degree depending on the selected trigonometric mode.
acosh(expr)
Area hyperbolic cosine.
atan(expr)
Arc tangent. Result is in radian or degree depending on the selected trigonometric mode.
atanh(expr)
Area hyperbolic tangent.
acot(expr)
Arc cotangent. Result is in radian or degree depending on the selected trigonometric mode.
acoth(expr)
Area hyperbolic cotangent.
binomial(n,k)
Binomial coefficient. Needs two parameters (n,k) , returns the number of k-combinations from a set with n elements.
Examples:
binomial(9,4)
Examples:
binomial(9,4)
ceiling(expr)
The least integer greater or equal to the given argument, if it is numerical.
Examples:
ceiling(4.3)
Examples:
ceiling(4.3)
char(m)
Characteristic polynomial of a matrix. First argument is the matrix, the second argument (which is optional) is a symbol. With only one argument the result will be a polynomial of x.
Examples:
char([2,1;3,5]) = x^2-7*x+7
char([2,1;3,8],y) = y^2-10*y+13
Examples:
char([2,1;3,5]) = x^2-7*x+7
char([2,1;3,8],y) = y^2-10*y+13
clear(symbol)
Clears any assigment previously made for the symbol given as the only argument.
Examples:
clear(x)
Examples:
clear(x)
coldim(m)
Number of columns in the matrix given as the single argument.
Examples:
coldim([1,2,3;2,3,4]) = 3
Examples:
coldim([1,2,3;2,3,4]) = 3
conj(expr)
Conjugate of a complex number.
Examples:
conj(3+2*i) = 3-2*i
Examples:
conj(3+2*i) = 3-2*i
cos(expr)
Cosine. Argument expected in radians or degrees depending on the selected trigonometric mode.
cosh(expr)
Hyperbolic cosine.
cot(expr)
Cotangent. Argument expected in radians or degrees depending on the selected trigonometric mode.
coth(expr)
Hyperbolic cotangent.
csc(expr)
Cosecant.
det(m)
Determinant of a matrix.
Examples:
det([2,1;3,5]) = 7
Examples:
det([2,1;3,5]) = 7
diff(expr,symbol[,n])
Computes the derivative of a function. First argument is the function, the second one is the variable. Third argument is optional, it determines how many times the function is differentiated.
Examples:
diff(x^2+x-1,x) = 2*x+1
diff(cos(x)*x*y,x) = y*(cos(x)-sin(x)*x)
diff(x^2+x,x,2) = 2
Examples:
diff(x^2+x-1,x) = 2*x+1
diff(cos(x)*x*y,x) = y*(cos(x)-sin(x)*x)
diff(x^2+x,x,2) = 2
dim(v)
Dimension of the vector given as the single argument. Works both with row and column vectors.
For matrices use the coldim and rowdim functions.
Examples:
dim([1,2,3]) = 3
For matrices use the coldim and rowdim functions.
Examples:
dim([1,2,3]) = 3
div(expr,expr)
Division with remainder. First argument is the dividend, second one is the divisor. The result consists of the quotient and the remainder. Arguments can be numbers or polynomials.
Examples:
div(9,4)
div(x^3+x^2-2x+1,x-1)
Examples:
div(9,4)
div(x^3+x^2-2x+1,x-1)
factor(expr)
Factorization of a polynomial.
Examples:
factor(x^2+x-2) = (x+2)*(x-1)
Examples:
factor(x^2+x-2) = (x+2)*(x-1)
factorial(n)
Factorial of an integer number.
Examples:
factorial(5) = 120
Examples:
factorial(5) = 120
floor(expr)
The greatest integer less or equal to the given argument, if it is numerical.
gcd(expr,expr)
Greatest common divisor of the two given arguments
Examples:
gcd(6,4)=2
gcd(x^2+2*x+1,x^2+3*x+2)=x+1
Examples:
gcd(6,4)=2
gcd(x^2+2*x+1,x^2+3*x+2)=x+1
ifactor(n)
Prime factorization of an integer number.
Examples:
ifactor(24)=2^3*3
Examples:
ifactor(24)=2^3*3
inv(m)
Inverse of a matrix.
Examples:
inv([2,1;5,3]) = [3,-1;-5,2]
Examples:
inv([2,1;5,3]) = [3,-1;-5,2]
invlap(expr,symbol,symbol)
Inverse laplace transform. Has three arguments:
- 1. The expression to be transformed.
- 2. Source variable (usually 's' in freq. domain)
- 3. Target variable (usually 't' in time domain)
Examples:
invlap(w/(w**2+s**2),s,t) = sin(w*t)
- 1. The expression to be transformed.
- 2. Source variable (usually 's' in freq. domain)
- 3. Target variable (usually 't' in time domain)
Examples:
invlap(w/(w**2+s**2),s,t) = sin(w*t)
im(expr)
Imaginary part of a complex number.
Examples:
im(3+2*i) = 2
Examples:
im(3+2*i) = 2
integrate(expr,symbol,expr,expr)
Computes the integral of a function. In case of definite integration you have to pass 4 arguments:
- 1. Integrand function
- 2. Variable of integration
- 3. lower bound of domain
- 4. upper bound of domain
The 3rd and 4th arguments can be omitted. In this case you get the indefinite integral.
Examples:
integrate(x^2,x) = x^3/3
integrate(sin(x),x,0,pi) = 2
- 1. Integrand function
- 2. Variable of integration
- 3. lower bound of domain
- 4. upper bound of domain
The 3rd and 4th arguments can be omitted. In this case you get the indefinite integral.
Examples:
integrate(x^2,x) = x^3/3
integrate(sin(x),x,0,pi) = 2
laplace(expr,symbol,symbol)
Laplace transform. Has three arguments:
- 1. The expression to be transformed.
- 2. Source variable (usually 't' in time domain)
- 3. Target variable (usually 's' in freq. domain)
Examples:
laplace(sin(w*t),t,s) = w / (w^2 + s^2)
- 1. The expression to be transformed.
- 2. Source variable (usually 't' in time domain)
- 3. Target variable (usually 's' in freq. domain)
Examples:
laplace(sin(w*t),t,s) = w / (w^2 + s^2)
lcm(expr,expr)
Least common multiple of the two given arguments
Examples:
lcm(12,15) = 60
lcm(2*x+1,3*x+2) = 6*x^2+7*x+2
Examples:
lcm(12,15) = 60
lcm(2*x+1,3*x+2) = 6*x^2+7*x+2
limit(expr,symbol,expr)
Limit of a function. If the two-sided limit does not exist returns right-side limit. It has 3 arguments:
- 1. Function.
- 2. Variable of the function.
- 3. The point of limit.
Examples:
limit(sin(x)/x,x,0) = 1
- 1. Function.
- 2. Variable of the function.
- 3. The point of limit.
Examples:
limit(sin(x)/x,x,0) = 1
limit2(expr,symbol,expr)
Two-sided limit of a function. If it does not exist returns undefined. It has 3 arguments:
- 1. Function.
- 2. Variable of the function.
- 3. The point of limit.
Examples:
limit2(sin(x)/x,x,0) = 1
limit2(1/x,x,0) = undefined
- 1. Function.
- 2. Variable of the function.
- 3. The point of limit.
Examples:
limit2(sin(x)/x,x,0) = 1
limit2(1/x,x,0) = undefined
limitl(expr,symbol,expr)
One-sided limit of a function from the left. It has 3 arguments:
- 1. Function.
- 2. Variable of the function.
- 3. The point of limit.
Examples:
limitl(1/x,x,0) = -infinity
- 1. Function.
- 2. Variable of the function.
- 3. The point of limit.
Examples:
limitl(1/x,x,0) = -infinity
limitr(expr,symbol,expr)
One-sided limit of a function from the right. It has 3 arguments:
- 1. Function.
- 2. Variable of the function.
- 3. The point of limit.
Examples:
limitr(1/x,x,0) = infinity
- 1. Function.
- 2. Variable of the function.
- 3. The point of limit.
Examples:
limitr(1/x,x,0) = infinity
ln(expr)
Natural logarithm. Has exactly one argument.
log(expr,expr)
Logarithm. Has two arguments, second one is the base.
Examples:
log(100,10) = 2
Examples:
log(100,10) = 2
log10(expr)
10-based logarithm. Has exactly one argument.
mateigen(m,symbol)
Eigenvalues and vectors of a matrix. First argument is the matrix, second is a symbol. The result is a list of lists of 3 elements, where the first element is a square free factor of the characteristic polynomial, the second its multiplicity and the third the corresponding eigenvector
Examples:
mateigen([1,2;2,1],x)
Examples:
mateigen([1,2;2,1],x)
matmake(expr,rsymbol,rn,csymbol,cn)
Creates a matrix. Requires exactly 5 arguments:
- 1. Expression to define the elements
- 2. Symbol to be substituted with the row number
- 3. Number of rows of the matrix
- 4. Symbol to be substituted with the column number
- 5. Number of columns of the matrix
Examples:
matmake(100a+b,a,3,b,4)
- 1. Expression to define the elements
- 2. Symbol to be substituted with the row number
- 3. Number of rows of the matrix
- 4. Symbol to be substituted with the column number
- 5. Number of columns of the matrix
Examples:
matmake(100a+b,a,3,b,4)
min(n,...)
Minimum of the arguments. Can also take a matrix or vector as an argument, in this case it returns its smallest element(s). If some of the arguments can be compared, more than one of them may be returned.
Examples:
min(10,-2,5)
min([2,6,1;2,4,5])
Examples:
min(10,-2,5)
min([2,6,1;2,4,5])
max(n,...)
Maximum of the arguments. Can also take a matrix or vector as an argument, in this case it returns its largest element(s). If some of the arguments can be compared, more than one of them may be returned.
Examples:
max(10,-2,5)
max([2,6,1;2,4,5])
Examples:
max(10,-2,5)
max([2,6,1;2,4,5])
nextprime(n)
Returns the next prime greater than the integer argument.
numint(expr,symbol,expr,expr)
Approximates the definite integral. Use it when integrate can't give you a result. Mandatory arguments:
- 1. Integrand function
- 2. Variable of integration
- 3. lower bound of domain
- 4. upper bound of domain
Examples:
numint(ln(x)/(x**4+1),x,2,4) = 0.0329272168747
- 1. Integrand function
- 2. Variable of integration
- 3. lower bound of domain
- 4. upper bound of domain
Examples:
numint(ln(x)/(x**4+1),x,2,4) = 0.0329272168747
numsolve(eq,symbol)
Returns an approximate solution of an equation, or a system of equations. Arguments are the equation(s) and the variable(s). The number of equations must be equal to the number of variables.
Only one solutions returned. When solving a single equation, an optional third argument can be the starting point of the Newton method.
Examples:
numsolve(x^4-ln(x)=2,x)
numsolve((x-2)^2=ln(x),x,1.5)
numsolve(ln(x)=y,x/5=y,x,y)
Only one solutions returned. When solving a single equation, an optional third argument can be the starting point of the Newton method.
Examples:
numsolve(x^4-ln(x)=2,x)
numsolve((x-2)^2=ln(x),x,1.5)
numsolve(ln(x)=y,x/5=y,x,y)
odesolve(expr,symbol,symbol)
Solves an ordinary differential equation. First argument is the equation, second is the function to be found, third is the independent variable.
Examples:
odesolve(diff(y,x,2)+y=0,y,x)
Examples:
odesolve(diff(y,x,2)+y=0,y,x)
partfrac(expr,symbol)
Partial fraction expansion. First argument is a fraction of two polynomials, second one is a variable. Returns the list of partial fractions.
Examples:
partfrac(x/(x+1),x) = 1 , -1/(x+1)
Examples:
partfrac(x/(x+1),x) = 1 , -1/(x+1)
pivot(m,r,c)
Returns the m matrix pivoted about the element in row 'r' and column 'c'.
Examples:
pivot([1,1,2;1,2,1;2,3,3],1,1)
Examples:
pivot([1,1,2;1,2,1;2,3,3],1,1)
prod(expr,symbol,expr,expr)
Product. Has 4 arguments:
- 1. Repeating term.
- 2. Index variable
- 3. Lower bound.
- 4. Upper bound
For example prod(x+2,x,1,3) = 60,
because it is equivalent to (1+2)*(2+2)*(3+2)
Examples:
prod(x+2,x,1,3)=60
- 1. Repeating term.
- 2. Index variable
- 3. Lower bound.
- 4. Upper bound
For example prod(x+2,x,1,3) = 60,
because it is equivalent to (1+2)*(2+2)*(3+2)
Examples:
prod(x+2,x,1,3)=60
random(n)
Random number. Returns a non-negative integer that is smaller than the argument. The value is drawn from a uniform distribution.
Examples:
random(10)
Examples:
random(10)
rank(m)
Rank of the matrix passed as the only argument.
Examples:
rank([1,1,2;1,2,1;2,3,3]) = 2
Examples:
rank([1,1,2;1,2,1;2,3,3]) = 2
re(expr)
Real part of a complex number.
Examples:
re(3+2*i) = 3
Examples:
re(3+2*i) = 3
roots(expr,symbol)
Roots of an expression. First argument is the expression, second one is a variable. Will returns the values of the variable where the expression is zero.
Examples:
roots(x^2+x-6,x)
Examples:
roots(x^2+x-6,x)
round(expr)
The nearest integer to the given argument, if it is numerical.
rowdim(m)
Number of rows in the matrix given as the single argument.
Examples:
rowdim([1,2,3;2,3,4]) = 2
Examples:
rowdim([1,2,3;2,3,4]) = 2
sec(expr)
Secant.
sign(expr)
The sign of the argument if it is numerical. Returns -1, 0 or +1.
sin(expr)
Sine. Argument expected in radians.
sinh(expr)
Hyperbolic sine.
solve(eq,symbol)
Solves an equation, or a system of equations. Arguments are the equation(s) and the unkown variable(s). There must be at least as many variables as equations.
Examples:
solve(x^2+x-6=0,x)
solve(x^2-3=y,x=y/2,x,y)
solve((a+b)/a=a/b,a,b)
Examples:
solve(x^2+x-6=0,x)
solve(x^2-3=y,x=y/2,x,y)
solve((a+b)/a=a/b,a,b)
sub(eq,expr)
Substitutes part of an expression by the given rule(s). First arguments are the rule(s), last is the expression.
Examples:
sub(x=y+1,x^2+1) = y^2 + 2*y +2
sub(x=z+2,y=z/2,x*y) = (z*(z + 2))/2
Examples:
sub(x=y+1,x^2+1) = y^2 + 2*y +2
sub(x=z+2,y=z/2,x*y) = (z*(z + 2))/2
sum(expr,symbol,expr,expr)
Summation. Has 4 arguments:
- 1. Repeating term.
- 2. Index variable
- 3. Lower bound.
- 4. Upper bound
For example sum(x^2,x,0,3) = 14,
because it is equivalent to (0^2+1^2+2^2+3^2)
Examples:
sum(x^2,x,0,3) = 14
- 1. Repeating term.
- 2. Index variable
- 3. Lower bound.
- 4. Upper bound
For example sum(x^2,x,0,3) = 14,
because it is equivalent to (0^2+1^2+2^2+3^2)
Examples:
sum(x^2,x,0,3) = 14
tan(expr)
Tangent. Argument expected in radians or degrees depending on the selected trigonometric mode.
tanh(expr)
Hyperbolic tangent.
taylor(expr,symbol,expr,n)
Taylor series of the given function. It has 4 arguments:
- 1. Function.
- 2. Variable of the function.
- 3. A point.
- 4. Maximum degree
Examples:
taylor(sin(x),x,1,3)
- 1. Function.
- 2. Variable of the function.
- 3. A point.
- 4. Maximum degree
Examples:
taylor(sin(x),x,1,3)
tp(m)
Returns the transpose of the matrix given in the argument.
Examples:
tp([3,4;1,2]) = [3,1;4,2]
Examples:
tp([3,4;1,2]) = [3,1;4,2]
trigsimp(expr)
Trigonometric simplifications. Needs one argument which is the expression to be simplified.
Examples:
trigsimp(sin(x)^2+cos(x)^2) = 1
Examples:
trigsimp(sin(x)^2+cos(x)^2) = 1
vlen(v)
The length (euclidean norm) of the vector given as the only argument
Examples:
vlen([1,2,3])
Examples:
vlen([1,2,3])
vdot(a,b)
Vector dot product. Arguments must be two vectors with the same size.
Examples:
vdot([1,2,3],[2,3,1])
Examples:
vdot([1,2,3],[2,3,1])
vcross(a,b)
Vector cross product. Arguments must be two three-dimensional vectors.
Examples:
vcross([1,1,0],[0,0,1])
Examples:
vcross([1,1,0],[0,0,1])
If you have any questions, problems or ideas about the application, feel free to contact the developer.
Filling out the e-mail field is optional.